Unit root test tính dừng kiểm tra tính ổn định dữ liệu, đây là một trong những kiểm định quan trọng trong phân tích định lượng, vì trong hồi quy muốn có dữ liệu chính xác thì các dữ liệu phải ổn định ở bậc gốc; Tức là trong mô hình sẽ không có hiện tượng hồi quy ảo, nhằm tăng tính chính xác cho kết quả hồi quy, song song đó khi dữ liệu không dừng ở bậc gốc thì chúng ta phải là gì ?
UNIT ROOT TEST
Test Tính dừng là gì ?
Trong thống kê , test tính dừng là kiểm tra xem biến chuỗi thời gian có phải là không ổn định và sở hữu nghiệm đơn vị hay không . Giả thuyết rỗng thường được định nghĩa là sự hiện diện của một gốc đơn vị và giả thuyết thay thế là gốc đứng yên , điểm dừng xu hướng hoặc gốc nổ tùy thuộc vào phép thử được sử dụng.
Các kiểm định cho tính dừng dữ liệu
Kiểm tra gốc đơn vị là kiểm tra tính ổn định trong một chuỗi thời gian. Chuỗi thời gian có tính ổn định nếu sự thay đổi về thời gian không gây ra sự thay đổi về hình dạng của phân bố; các gốc đơn vị là một trong những nguyên nhân dẫn đến tính không ổn định.
Các thử nghiệm này được biết đến là có sức mạnh thống kê thấp . Nhiều thử nghiệm tồn tại, một phần, bởi vì không có thử nghiệm nào nổi bật là có sức mạnh nhất . Các bài kiểm tra bao gồm:
- Phép thử Dickey Fuller (đôi khi được gọi là phép thử Dickey Pantula), dựa trên hồi quy tuyến tính . Tương quan nối tiếp có thể là một vấn đề, trong trường hợp đó có thể sử dụng thử nghiệm Augmented Dickey-Fuller (ADF) . ADF xử lý các mô hình lớn hơn, phức tạp hơn. Nó có nhược điểm là tỷ lệ lỗi Loại I khá cao .
- Bài kiểm tra Elliott – Rothenberg – Stock , có hai kiểu phụ: P-test có tính đến mối tương quan nối tiếp của thuật ngữ lỗi , Thử nghiệm DF-GLS có thể được áp dụng cho dữ liệu bị loại bỏ mà không bị chặn.
- Kiểm định Schmidt – Phillips bao gồm các hệ số của các biến xác định trong giả thuyết rỗng và giả thuyết thay thế . Các kiểu phụ là bài kiểm tra rho và bài kiểm tra tau .
- Phép thử Phillips – Perron (PP) là một sửa đổi của phép thử Dickey Fuller, và sửa lỗi tự tương quan và phương sai thay đổi .
- Kiểm tra Zivot-Andrews cho phép phá vỡ tại một điểm không xác định trong xu hướng đánh chặn hoặc tuyến tính .
Hệ quả của dữ liệu không ổn định
Lý do tại sao nó được gọi là một đơn vị gốc là vì toán học đằng sau quá trình. Ở cấp độ cơ bản, một quá trình có thể được viết dưới dạng một chuỗi các đơn thức (biểu thức với một số hạng duy nhất). Mỗi đơn thức tương ứng với một căn . Nếu một trong các gốc này bằng 1, thì đó là một gốc đơn vị.
Phép toán đằng sau đơn vị gốc nằm ngoài phạm vi của trang web này. Tất cả những gì bạn thực sự cần biết nếu đang phân tích chuỗi thời gian là sự tồn tại của nghiệm đơn vị có thể khiến phân tích của bạn gặp các vấn đề nghiêm trọng như:
- Hồi quy giả : bạn có thể nhận được giá trị bình phương r cao ngay cả khi dữ liệu không liên quan.
- Hành vi sai sót do các giả định để phân tích không hợp lệ. Ví dụ, tỷ số t sẽ không tuân theo phân phối t
Cách kiểm tra tính ổn định dữ liệu.
Để kiểm tra tính dừng của số liệu thì có nhiều phần mềm, phần lớn các phần mềm thống kê điều có thể làm được, nhưng trong bài viết này chúng tôi sử dụng phần mềm Eviews để cho các bạn dễ hình dùng, nếu sử dụng được trên Eviews thì vấn đề sử dụng trên phần mềm đồ hoạ tác tác khác cũng đơn giản, ngày cả những phần mềm dòng lệnh như Stata, R … cũng không làm khó bạn.
Vẽ đồ thị
Dữ liệu mang tính chất ổn định sẽ giao động quanh một trục cố định và có tính chất xu hướng đi ngang; Còn ngược lại dữ liệu không ổn định thì sẽ có xu hướng đi lên hoặc xuống.

Ta dễ dàng nhận thấy rằng, dữ liệu đang giao động quan trục giá trị 4 và có xu hướng đi ngang. => Dữ liệu ngày có tính dừng.
Kiểm định unit root test
Dữ liệu 1 chiều
Mở dữ liệu cần kiểm tra trong Eviews lên
View > Unit Root test
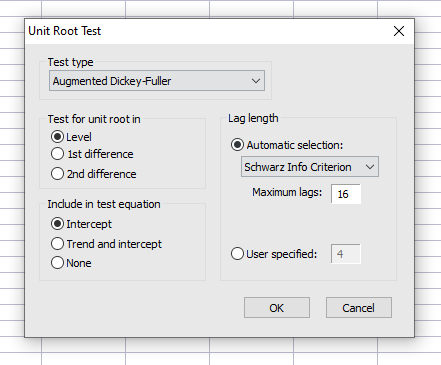
Test type: Phương pháp kiểm định, thứ tự là tính phổ biến của kiểm định (Tôi nhắc lại là tính phổ biến, không phải tốt hơn hay dở hơn).
- The Augmented Dickey-Fuller (ADF) Test
- Dickey-Fuller Test with GLS Detrending (DFGLS)
- The Phillips-Perron (PP) Test
- The Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) Test
- Elliot, Rothenberg, and Stock Point Optimal (ERS) Test
Test for unit root: chọn bậc sai phân dữ liệu
- Level: bậc gốc
- 1st difference: sai phân bậc 1
- 2nd difference: sai phân bậc 2
Dữ liệu của mình bằng mọi giá phải dừng ở sai phân bậc gốc (không sai phân) hay sai phân bậc 1 thôi.
Include in test equation: thành phân thêm trong lức tính hồi quy
- Intercept: bao gồm hệ số chặn
- Trend & Intercept: Có tính xu hướng và hệ số chặn
- None: Không xu hướng và không hệ số chặn
Chưa có tài liệu nào có những quy định cụ thể về thành phần khi chạy tính dừng cả, nên các bạn lựa chọn làm sao cho kết quả phù hợp với nhu cầu phân tích data của bạn.
Automatic Selection: chỉ tiêu chất lượng
Thông thường chọn AIC, vì tôi thấy không ai quan tâm đến chỉ tiêu chất lượng này cả
Có 1 công bố khoa học, nói về các chỉ tiêu đi kèm với loại dữ liệu. ( Nhưng lâu quá tối không còn giữ tài liệu này, để show lên cho các bạn, nhưng nó cũng không quá quan trọng, bởi vậy các bạn cứ chọn AIC)
Max lag: độ trễ tối đa
Để mặc định theo dữ liệu do phần mềm Eviews tính.
Bây giờ lựa chọn và chạy kiểm định tính dừng thôi
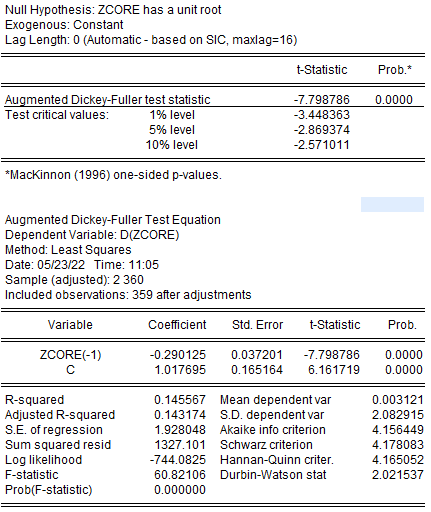
Giá định:
- H0: Dữ liệu không ổn định
- H1: Dữ liệu đã ổn định
Ta có Pvalue (Prob) < 0.05, Ta bác bỏ H0 và chấp nhận H1, Tức dữ liệu đã dừng ở bậc gốc
Dữ liệu 2 chiều ( dữ liệu bảng (Panel))
Khi chạy unit root test cho dữ liệu panel thì chúng ta cũng thực thiện tương tương như unit root test bình thường

Nó chỉ khác là dạng của kiểm định ( tên kiểm định là khác):
Bây giờ gồm:
- test của Levin – Lin -Chu
- test của Breitung
- Test của Im Pesaran Shin
- Test của Fisher – ADF
- Test của Fisher – PP
Nó chỉ khác là những người phát triển test thôi ( phương pháp test khác nhau).
Tính dừng cho dữ liệu mùa vụ
Hiện tại chức năng này chỉ có từ Eviews 11, nên các bạn cần phải sử dụng những phần mềm câu lệnh như Stata hay R để tính toán.
Kết luận
Tính dừng của dữ liệu là một kiểm định rất cần thiết khi các bạn chạy các mô hình định lượng thời gian như: hồi quy ols, hồi quy panel, dự báo Arima, dự báo Holtwinters, dự báo harmonic, mô hình VAR, mô hình VECM, mô hình FMOLS, mô hình ADRL….
Nếu các bạn gặp khó khăng trong việc chạy định lượng ứng dụng vào nghiên cứu khoa học: luận văn thạc sĩ, luận án tiến sĩ, đề tài khoa học, công bố khoa học …Các bạn hãy liên hệ với chúng tôi, để được tư vấn và hỗ trợ kịp thời.


Có thể bạn thích bài viết này:
[Đào tạo] khoá học xử lý số liệu & phân tích định lượng Stata SmartPLS SPSS R-Studio
Khoá học xử lý số liệu & phân tích định lượng Stata SmartPLS SPSS R-Studio [...]
Th5
Chỉnh sửa định dạng văn bản in ấn tài liệu lưu hành nội bộ Thủ Đức TpHCM
Chỉnh sửa định dạng văn bản in ấn tài liệu lưu hành nội bộ Thủ [...]
Th4
Làm data khảo sát trực tuyến dữ liệu luận văn thạc sĩ giá rẻ
Làm data khảo sát trực tuyến dữ liệu luận văn thạc sĩ giá rẻ ! [...]
Th3
Nhận làm đẹp data làm sạch dữ liệu hồi quy ols tobit probit efa logit
Nhận làm đẹp data làm sạch dữ liệu hồi quy ols tobit probit efa logit [...]
Th3
9 chỉ tiêu đánh giá độ chính xác mô hình hồi quy
Để đánh giá độ chính xác của mô hình hồi quy, chúng ta cần sử [...]
Th3
top 5 phần mềm thống kê: xử lý số liệu phân tích dữ liệu
top 5 phần mềm thống kê: xử lý số liệu phân tích dữ liệu; Đây [...]
Th3
Mô hình chấp nhận thông tin (Information Adoption Model – IAM)
Mô hình chấp nhận thông tin (Information Adoption Model – IAM), đây cũng là một [...]
Th2
Kinh tế tân cổ điển mô hình Solow – Swan
Mô hình kinh tế tân cổ điển, thuyết kinh tế Solow – Swan là một [...]
Th2